基于行星滾柱絲杠副的機電作動器動態特性分析
2017-5-5 來源:西北工業大學 作者:喬冠,劉更,馬尚君,佟瑞庭,周勇
摘要: 以舵回路系統中機電作動器為研究對象,考慮機電作動器的安裝和舵面負載連接,建立了基于行星滾柱絲杠副的機電作動器數學模型。采用 AMESim 進行仿真對比分析,探討了機電作動器中結構剛度、摩擦和間隙等非線性因素對系統動態性能的影響。結果表明: 相比傳動剛度,結構剛度中固定剛度的提高對于系統動態響應的改善作用更明顯; 行星滾柱絲杠副間隙量越大,系統的階躍響應波動幅值越明顯; 在給定舵控指令下,機電作動器的仿真位移輸出響應誤差最大為 1. 8 mm,相對誤差為 1. 2% ,從而較好的反映了模型的有效性,為功率電傳機電作動器的進一步結構優化和控制提供理論依據。
關鍵詞: 機電作動器; 行星滾柱絲杠副; 動態特性; 結構剛度; 間隙非線性
機電作動器( Electro-Mechanical Actuator,EMA) 是功率電傳作動系統的一個分支,由于其具有重量輕、工作效率高、系統可靠性高和便于維護[1 - 2]等優點,廣泛應用于飛行舵面控制、推力矢量控制、飛機剎車和工業過程控制等軍民領域。國外在 EMA 動態特性研究方面起步較早,建立了EMA 系統級功率鍵合圖模型和基于 AMESim 環境的EMA 仿真模型,對采用反向式行星滾柱絲杠副的 EMA進行動態性能測試,通過力矩和轉速干擾實驗驗證模型的有效性[3]。Karam 等[4]討論了力控制的基于行星滾柱絲杠副的 EMA 中摩擦、轉子慣量和測試平臺剛度等因素的影響,這些因素都會改變 EMA 的穩態和動態特性。Mare 等[5 - 6]提出基于仿真模型的 EMA 率傳遞初步設計準則,以確保測試平臺結構與目標動態性能的一致,考慮了結構部件的靜態與動態性能的限制,從而使得控制器設計更簡單。Habibi 等[7]分析了控制飛機舵面的 EMA 動態特性,表明由空程和靜態摩擦產生的死區是限制 EMA 輸入輸出特性的重要因素,并通過使用內環控制策略減小死區對系統的影響。國內 20世紀 90 年代初才開始研究包括機電作動器和電動靜液作動器( Electro-Hydrostatic Actuator,EHA) 在內的功率電傳作動器,已證實該技術的可行性和有效性。齊海濤等[8]基于 AMESim 對 EHA 進行了建模和仿真分析,仿真結果表明所設計的 EHA 動態性能良好,達到了預定的性能指標。馬尚君等[9]建立了 EMA 中的標準式行星滾柱絲杠副有限元模型,基于顯式動力學有限元算法對其動態特性進行仿真分析,為研究 EMA 整體性能的提高提供參考。國內學者多數的研究工作集中于 EMA 的復合式余度控制[10]、混合作動系統研究[11]等方面,然而對基于行星滾柱絲杠副的 EMA 中結構剛度、摩擦和間隙因素對 EMA 動態特性影響研究較少涉及,鮮有文獻報道考慮 EMA 的安裝和舵面負載連接并建立數學模型。
本文考慮 EMA 的安裝、EMA 與舵面負載的連接,建立了基于行星滾柱絲杠副的 EMA 數學模型。采用AMESim 仿真分析,分別探討了舵回路系統中 EMA 的結構剛度、摩擦和間隙等非線性因素對系統的動態性能影響。在相同給定的舵控指令下,對比本文 EMA 與傳統伺服油缸的位移跟蹤精度,結果表明建立的 EMA模型是有效的。
1.EMA 系統組成
1. 1 EMA 結構形式
典型的 EMA 在飛行器舵回路系統中的組成見圖1,EMA 主要由無刷直流電機、控制器( 主要包括速度、位置控制器和功率變換器) 、齒輪減速器( 或者帶傳動) 、滾珠絲杠副( 或者行星滾柱絲杠副) 這四部分組成。其中,滾珠絲杠副( Ball Screw Mechanism,BSM) 和行星滾 柱絲 杠 副 ( Planetary Roller Screw Mechanism,PRSM) 作為 EMA 中的執行機構,用來傳遞扭矩、進行運動變換。PRSM 用滾柱作為中間傳動體,用滾動摩擦取代滑動摩擦,具有效率高、壽命長、承載能力強等特點。其中,標準式行星滾柱絲杠副( Standard PlanetaryRoller Screw Mechanism,SPRSM) 主要傳動裝置有絲杠、螺母和滾柱,其基本結構見圖 2。本文以基于 SPRSM 的EMA 為對象建模并進行其動態特性研究分析。
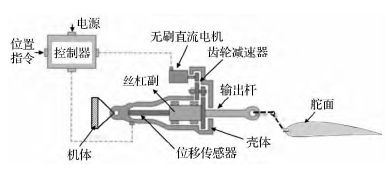
圖 1 舵回路系統中的 EMA 結構

圖 2 SPRSM 基本結構
1. 2 EMA 在舵回路系統中的工作原理
EMA 通過鉸鏈安裝于機體,并由其輸出桿帶動搖臂等連接機構,最終實現舵面的位置控制( 見圖 1) 。控制器接受來自飛控計算機的舵控指令,驅動無刷直流電機做正反向運動,再通過齒輪裝置減速增扭,把絲杠的旋轉運動轉化為輸出桿相對于殼體的直線運動,驅動舵面實現相應的動作。同時,電機中的電流信號,電機輸出軸的轉速信號和舵面的位置信號都通過反饋參與到控制器的運算實現閉環反饋控制。
2.EMA 系統建模
結合圖 1,在 AMESim 中建立的 EMA 整個系統模型見圖 3,部分子模型采用超級元件封裝。EMA 的建模主要包括: “a”為正弦或給定的信號指令輸入; “b”和“c”分別為電機控制器和無刷直流電機數學模型;“d”和“e”分別為齒輪副和 SPRSM 的機械傳動模型;“f”和“g”為考慮作動器固定機構和連接機構的等效剛度和阻尼; “h”為舵面及氣動力負載模型。
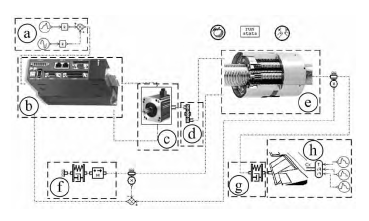
圖 3 EMA 系統模型
2. 1 控制器模型
控制器是 EMA 的重要組成部分,為防止電樞電流過載,保證電機的響應速度和動態特性,控制器采用電流、速度雙閉環,兩環均采用 PI 控制; 位置環采取簡單的比例控制( 見圖 4) 。該模型還包括信號采樣、電壓電流限幅以及力閉環反饋等。
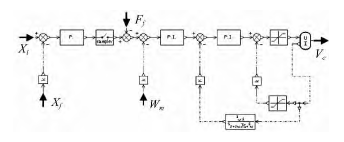
圖 4 控制器模型
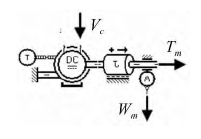
圖 5 電機模型
2. 2 電機模型
采用 270 V 永磁無刷直流 電 機,選 用 AMESim電機及驅動庫中的直流電機模型( 見圖 5) 。參照表1,電機的電樞電流 Ic與輸入電壓 Vc的關系通過一個一階傳遞函數 Ge描述


表 1 電機的相關參數設置
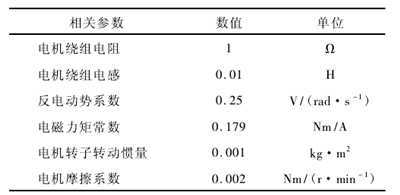
2. 3 SPRSM 模型
SPRSM 模型考慮了部件的移動和轉動部分,并綜合計入了摩擦和間隙非線性因素。EMA 中的摩擦非線性影響是降低系統控制性能因素之一。由于單獨分離

式( 6) 和式( 7) 中的 l 為 SPRSM 的導程,Fext為負載端承受的外力,Ffric為輸出桿端的整體摩擦力。EMA的整體摩擦力是外力和電機轉速的函數。為了簡化復雜的因果關系,可通過式( 8) 對整體摩擦力進行建模,該模型考慮了負載端承受的外力。

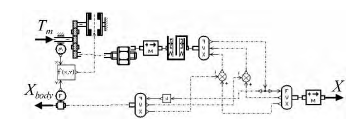
圖 6 SPRSM 的三端口模型
2. 4 舵面模型
AMESim 是面向對象的液壓 / 機械系統建模、仿真及動力學分析軟件。本文在建立舵面模型時,選用其平面機構庫中的模型模擬舵面的實際情況。包括舵面安裝鉸鏈、舵面質心、加載位置及搖臂的建模等,提供了更豐富的力與力矩加載( 見圖 7) 。這樣不僅可以仿真舵面的負載特性,還可以通過三維可視化功能AMESim-Animation 觀察舵面的實際運動情況。
3.EMA 動態特性分析
設置控制指令為 0.1 s 時刻的 0.1 V 階躍信號,經轉化比例系數,即為 1 mm 階躍信號,系統仿真時間為10 s,在 5 s 時加入 10 000 N 的階躍沖擊力,參數見表 1和表 2。
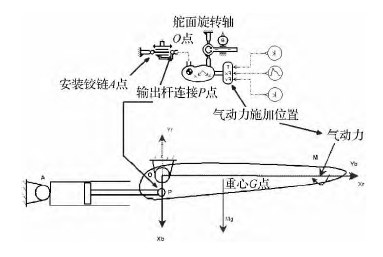
圖 7 舵面模型
表 2 EMA 系統的相關參數設置

3.1 傳動間隙非線性因素影響
間隙是限制速度與位置控制性能高低的最重要非線性影響因素之一。EMA 的間隙主要包括 PRSM 中絲杠側與螺母側的軸向間隙,齒輪傳動中的齒側隙和軸承軸向間隙等。間隙的存在使得 EMA 在反向作動時產生作動器位置輸出誤差,影響作動器位置輸出精度。由于傳動鏈中尺寸誤差、安裝誤差和長期磨損,間隙不能完 全 消除。間隙非線性 可以 采用 Physical 模 型、Phase plane 模型Dead zone 模型和 Rubber 模型來表示。Dead zone 模型是 Physical 模型的簡化,在轉軸無阻尼 或 小 阻 尼 時 Dead zone 模 型 是 一 種 有 效 的 模

此時軸的模型假設為純彈簧,不計慣量和內部阻尼,并且在不接觸時處于穩定狀態( 見圖 8) 。如果考慮軸的內部阻尼,修正的 Dead zone 模型如式( 13) 。
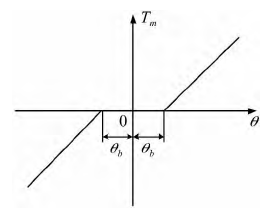
圖 8 Dead zone 模型


圖 9 間隙值為 0. 002 mm 的系統階躍響應
對比圖 9 ~ 圖 11 的三條系統響應曲線可知,不同大小的間隙值對系統的影響程度不同,間隙量越大,系統的階躍響應波動幅值越明顯。在 EMA 中,間隙影響的不僅是控制精度,還對系統的穩定性產生重大影響。為改善 EMA 的動態輸出響應,從機械方面,采用消隙齒輪結構,對 PRSM 預緊; 從材料方面,采用抗磨損材料; 從控制方面,通過軟件和控制策略 進行間 隙 補償等。
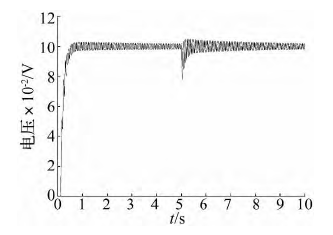
圖 10 間隙值為 0. 02 mm 的系統階躍響應
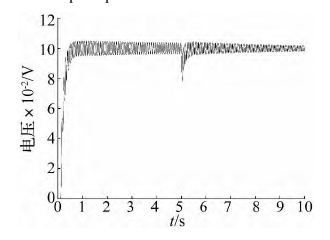
圖 11 間隙值為 0. 05 mm 的系統階躍響
3. 2 摩擦非線性因素影響
采用前述圖 6 建立的 SPRSM 摩擦模型,由式( 9) 可求得摩擦力矩,圖 12 比較了考慮摩擦和不考慮摩擦模型的系統階躍響應,此時假設機械傳動中不存在間隙。
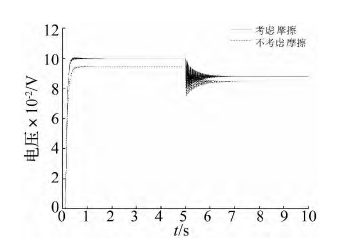
圖 12 考慮摩擦和不考慮摩擦模型的響應對比圖
可見,考慮摩擦的系統存在更大的誤差,應通過力閉環反饋改善。在 AMESim 模型中的等效連接結構與舵面間加入力傳感器,將測量到的力信號反饋到控制器形成閉環( 見圖 13) 。同時在反向通道內加入一階低通濾波器,結構為
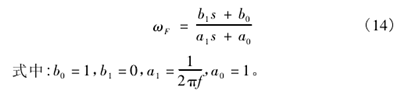
從圖 14 可知,加入力閉環反饋后,響應曲線的振蕩幅值小于無力閉環反饋的工況,同時系統的靜態誤差減小。同樣,常用減小機械系統中摩擦的方式可改善運動部件的潤滑條件,采用抗摩擦材料以及軟件進行摩擦補償等

圖 13 加入力反饋的 EMA 模型
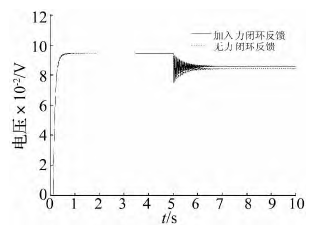
圖 14 考慮力閉環反饋的系統響應對比圖
3. 3 固定剛度和傳動剛度的影響
實際舵回路系統中,機體和被控舵面的剛度并不是無限大。本文在 EMA 系統建模時采用集中參數法考慮了殼體與機體間和輸出桿與舵面負載間的彈簧效應。由于負載系統中含有以柔性結構相連的多級共振性負載,因此 EMA 殼體和舵面不能簡單采用單質量 -單彈簧系統近似,而應考慮輸出桿與被控舵面間的傳動剛度和固定殼體的固定剛度( 統稱為結構剛度)[13]。KZ1為固定剛度; KZ2為傳動剛度。從圖 15 ~ 圖 16 可知,結構剛度對 EMA 的動態性能影響較大。當固定剛度和傳動剛度均為 1 × 107N / m時,系統的階躍響應存在小幅值振蕩,在 5 s 時刻施加10 000 N 的階躍沖擊力會使系統振蕩的幅值更劇烈,不利于系統的快速穩定。從圖 17 可知,此時的諧振頻率為 7. 75 Hz,此振蕩頻率由 2 000 kg 的舵面質量,與一條等效彈簧串聯得到。
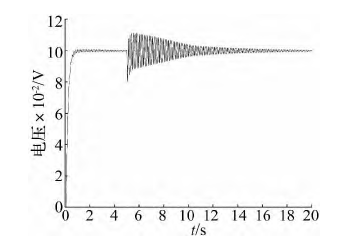
圖 15 固定剛度和傳動剛度均為 1 × 107N / m 時系統階躍響應
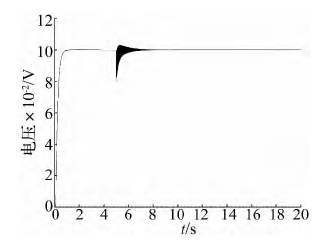
圖 16 固定剛度和傳動剛度均為 5 × 108N / m 時系統階躍響應

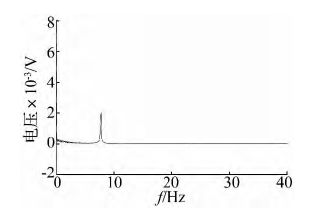
圖 17 固定剛度和傳動剛度均
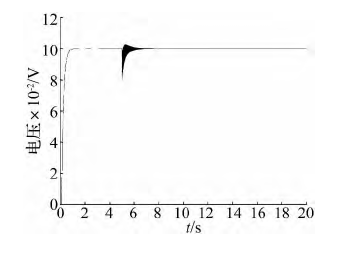
圖 18 固定剛度和傳動剛度為 1 × 109N / m 時系統階躍響應
另一方面,從圖 19 ~ 圖 22 可知,當傳動剛度為 1 ×107N / m 時,提高固定剛度可以明顯提高系統的動態響應,而當固定剛度提高到 1 × 109N / m 時,已經和固定剛度為 5 × 108N / m
時的系統動態響應無明顯區別。同樣,當固定剛度為 1 × 107N / m 時,提高傳動剛度也可以在一定程度上提高系統的動態響應,但即使當傳動剛度為 1 × 109N / m,系統的階躍響應依然存在大范圍的振蕩。通過以上分析可知,固定剛度的提高對于系統動態響應的改善作用更明顯。為保證 EMA 在工作過程中的信號跟蹤能力,除采用必要的控制策略外,在結構方面應適當優先提高固定剛度。
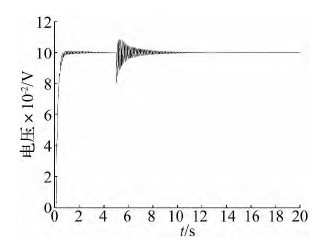
圖 19 固定剛度為 5 × 108N / m 傳動剛度為 1 × 107N / m 時系統階躍響應
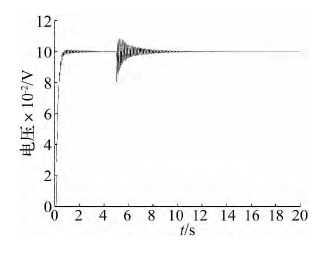
圖 20 固定剛度為 1 × 109N / m 傳動剛度為 1 × 107N / m 時系統階躍響應
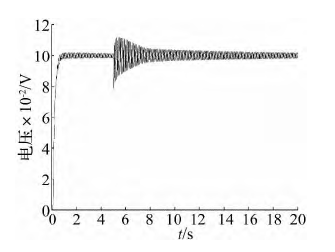
圖 21 固定剛度為 1 × 107N / m 傳動剛度為 5 × 108N / m 時系統階躍響應
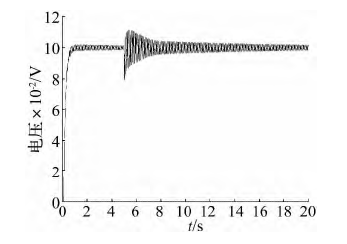
圖 22 固定剛度為 1 × 107N / m 傳動剛度為 1 × 109N / m 時系統階躍響應
3. 4 EMA 系統動態仿真
根據 EMA 實際舵控經驗,給定位移信號,參數如前述表 1 和表 2,設置仿真時間為 200 s,仿真步長為 0.001 s,得到的仿真結果見圖 23。從圖 23 ~ 圖 24 可知,系統的響應時間能夠滿足要求,系統動態跟蹤性能良好。

圖 23 EMA 仿真輸出位移跟蹤曲線
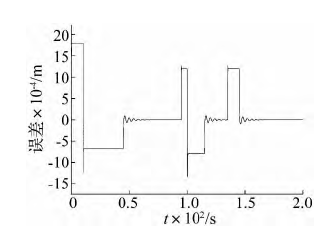
圖 24 位移跟蹤誤差曲線
在 200 s 的時間內,EMA 的輸出位移與給定位移信號的誤差最大為 1. 8 mm,相對誤差為 1. 2% ,從而較好的反映了模型的有效性。同時,對比本文中 EMA 與文獻[14]所述的傳統閥控液壓作動器,在給定相同舵控指令下,這兩種作動器都能跟蹤給定位移信號,但就跟蹤效果而言,傳統的閥控液壓作動器要優于 EMA,這也正是目前液壓作動器存在的主要原因。然而,在重量、體積、系統效率和可維護性等方面,EMA 有絕對優勢。
4.結論
采用 AMESim 圖形化建模方法,建立了基于 PRSM的 EMA 模型,對其在舵回路系統中的動態特性進行了仿真分析,得出以下結論:( 1) 傳動間隙和摩擦特性是限制系統精度和穩定性的重要非線性影響因素。間隙的存在使得系統振蕩不利于快速穩定,間隙量越大,系統的階躍響應波動幅值越明顯; PRSM 中的摩擦使得系統存在靜態誤差,可通過力閉環反饋減小其對系統的影響。( 2) 固定剛度和傳動剛度對 EMA 動態階躍特性有不同程度的影響,建議把安裝結構和傳動結構的剛度設計在 108N / m 的量級; 通過對比可知,固定剛度的提高對于系統動態響應的改善作用更明顯,在結構設計方面應適當優先提高固定剛度。( 3) 在給定舵控指令下,機電作動器的仿真位移輸出響應誤差最大為 1. 8 mm,相對誤差為 1. 2% ,從而反映了模型的有效性
。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息




