電主軸是機床主軸與主軸電機“合二為一”的傳動結構形式,它具有結構緊湊、轉速高、易于平衡和傳動效率高等優點。電主軸是高速數控機床的核心部件。在電主軸可靠性設計和試驗中,電主軸典型用戶載荷不僅是必不可少的前提條件,而且也是電主軸可靠性試驗平臺構建的關鍵科學依據。目前,電主軸作為高速機床的主軸部件,其還是多靠經驗設計,缺乏全面真實的外載荷依據,還沒有建立起電主軸載荷譜,不僅無法實現電主軸可靠性設計,而且構建可靠性試驗平臺也缺乏科學的依據[1]。在國內外,電主軸本身載荷譜的研究目前還是一個空白, 20 世紀末,吉林工業大學開展過數控車床載荷譜的研究,為進一步開展數控機床載荷譜研究提供了參考。2007 年,北京工業大學進行立式加工中心可靠性測試與評價技術的研究,其中涉及立式加工中心可靠性試驗載荷譜的研究。
根據開展國產170XD30 銑削電主軸可靠性試驗的需要,對該銑削電主軸典型用戶的零件圖、銑削工藝等( 例如: 主軸轉速、銑削用量、進給速度) 進行調研和收集,對相關切削數據進行了分析和計算,整理出了該電主軸載荷譜的樣本數據,初定總體分布類型和參數估計,最后運用K-S 檢驗法進行分布擬合檢驗,建立了該銑削電主軸載荷譜的數學模型和五級試驗程序加載譜,為開展其可靠性加載試驗提供科學的依據。
1 載荷的獲取
建立國產170XD30 銑削電主軸的載荷譜,其中該電主軸主要的技術參數包括: 最高轉速為30 000 r/min,額定功率為22 kW,采用油氣潤滑和HSK 刀具接口。載荷譜指的是載荷的時域分布規律,就是將復雜多變,雜亂無章的工況的實際載荷數據,加以統計和分析整理,研究這些載荷數據的規律性,以一定的圖像,表格或者數學式表示就是所謂的載荷譜。載荷是一個廣義的概念,可以是力、力矩、位移、應力、應變等[2]。在電主軸銑削加工過程中,電主軸的受力有銑削力,離心力和熱應力等。其中銑削力屬于電主軸的外載荷,而離心力和熱應力是電主軸的內載荷,根據電主軸可靠性試驗加載的需要,電主軸載荷譜關注的是電主軸的外載荷,同時參考文獻[2]數控車床載荷譜的建立,最終確定該電主軸載荷為銑削扭矩,對應的作用時間為加工一個工步的作用時間。該電主軸載荷譜的建立是以電主軸所受相對扭矩( 電主軸所受某一扭矩與其所受最大扭矩的比值) 和相對銑削時間( 電主軸所受某一扭矩的切削時間與電主軸所有扭矩的切削時間和的比值) 為統計量。那么,其載荷譜建立的關鍵是要取得電主軸的銑削扭矩和相應的銑削時間。
電主軸載荷數據的獲取是建立其載荷譜的基礎,載荷數據可以通過現場測試或者工藝分析計算獲取,本文采用工藝分析計算的方法獲取[2]。工藝分析計算的方法如下: 調研和收集國產170XD30 銑削電主軸典型用戶( 模具行業、汽車行業等) 的典型零件有關工藝數據,并根據收集到的工藝參數,計算其銑削力、銑削扭矩、相應的銑削時間,進而計算相對扭矩,相對銑削時間等。由于實際情況的復雜性,通過公式計算的載荷值與實際值具有一定的誤差,但是載荷譜的建立是以載荷的相對值為基礎,這樣就防止了由于公式計算的誤差而導致的電主軸載荷譜變化規律的不真實性。所以本文采用分析計算的方法來獲取銑削電主軸所受的載荷數據。為此,我們對國產170XD30 銑削電主軸銑削工藝和銑削參數進行了大量的調研和收集。
2 載荷的計算和統計
2. 1 銑削力的計算
由于銑削過程的復雜性,影響它的因素有很多,目前尚未有簡便的計算銑削力的公式,一般都是通過大量試驗,由測力儀測得銑削力后,根據銑削條件進行數據處理,然后得出經驗的計算公式[3]。目前,在實際生產中,用指數公式進行銑削力的計算在實際中得到了廣泛應用。

對于其它形狀的銑削工件,在分析工件銑削工藝的基礎上,可將銑削工件的表面劃分成多個長方形平面,計算每一個長方形平面的銑削時間Ti,則ΣTi就是所求的銑削時間。
2. 5 相對銑削時間計算
![]()
式中: T 為銑削時間,s; ΣT 為銑削時間的總和,s。
2. 6 載荷的統計
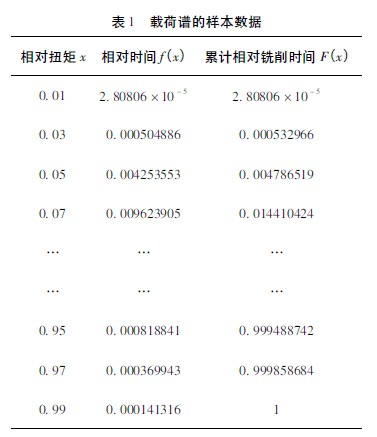
根據以上計算公式對采集、調研、整理的銑削工藝數據進行分析和計算,分組后得到的相對扭矩x、相對銑削時間f ( x) 和累積相對銑削時間F( x) 如表1 所示,它將作為建立該電主軸載荷譜的樣本數據[4]。
3 數據處理與參數估計
3. 1 繪制分布點圖
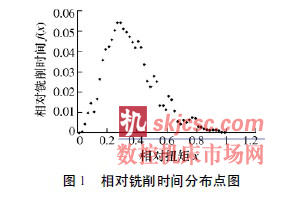
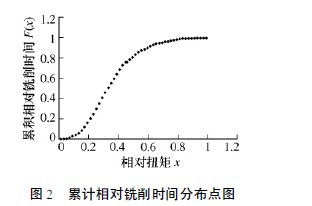
繪制分布點圖是整理數據最基本的方法之一,通過分布點圖可以清楚地看出樣本的分布情況,并可用來估計總體的分布情況。對表1 整理出的數據,以相對銑削扭矩x 為橫坐標,以每組內的相對銑削時間f( x) 為縱坐標,繪制出相對銑削時間分布點圖( 圖1 所示) ; 以相對銑削扭矩x 為橫坐標,以每組內的累計相對銑削時間F( x) 為縱坐標,繪制出累計相對銑削時間分布點圖( 圖2 所示) 。
3. 2 初定分布類型
初定分布類型就是根據樣本繪制出的頻率分布點圖和累計頻率分布點圖,來初步判斷樣本數據符合哪種分布。本文從常用的幾種統計分布模型中初選了3 種分布模型,3種分布模型分別是伽瑪分布、正態分布和貝塔分布[5]。其中伽瑪分布密度函數為

式中: α 為形狀參數; β 為尺度參數。初選分布模型后,需對各種模型分別進行參數估計,最后確定符合樣本數據的最佳分布模型。
3. 3 分布模型的參數估計
參數估計的方法有點估計、區間估計等。其中點估計法又可分為圖估計法、矩法、極大似然法等。矩法估計直觀又簡單,對任意總體都可用之[5]。本文選擇矩法對初選模型進行參數估計。
矩法估計是用樣本各階原點矩的函數來估計總體各階原點矩同一函數的方法,樣本的一階矩可做為總體均值μ 的點估計,樣本的二階中心矩可做為總體方差σ2 的點估計,本文求樣本均值μ- 與方差σ - 2 的公式為

根據以上公式,代入樣本的均值μ- 和方差σ - 2,估計出初定3 種分布模型的參數。表2 所列數據是3種分布模型的估計參數。表中a、b 分別表示各種分布的形狀參數和尺度參數。
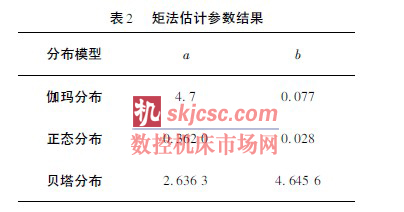
圖3 ~ 圖8 分別是根據表2 所估計參數繪制了伽瑪分布、正態分布和貝塔分布的理論概率密度函數曲線和累計分布函數曲線。其中,虛線是樣本數據的分布點圖,實線是繪制的理論分布曲線。
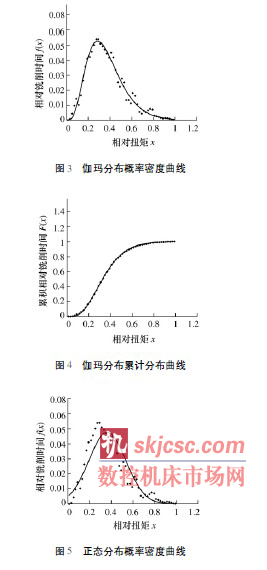
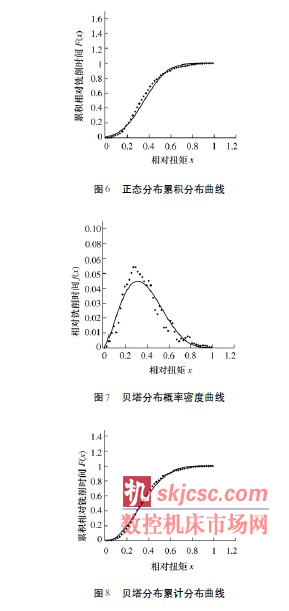
4 分布檢驗
通過前幾節的論述,對初定的3 種分布模型進行了參數估計,那么,總體到底符合哪種分布模型?就要對初定的發布模型進行假設檢驗。在數理統計中,K-S 檢驗法是一種常用且較為準確的假設檢驗方法,所以本文采用K-S 檢驗法對初定3 種模型進行檢驗,但是K-S 檢驗法僅檢驗理論累積分布函數和樣本的分布函數的誤差,并沒有檢驗理論概率密度函數和樣本的概率密度函數之間的誤差。因此,本文在K-S 檢驗法的基礎上,同時也進行了分布模型的概率密度函數誤差的檢驗。最符合總體分布模型的具體檢驗判據如下:
1) 通過K-S 檢驗法的檢驗并且K-S 檢驗法的統計量Dmax的值最小。
2) 理論分布模型和樣本數據概率密度函數的誤差平方和最小[4,6]。
如果檢驗結果不能同時滿足以上兩點判據,這就可能與樣本數據的容量多少、樣本數據的光滑、分組、初定理論分布模型不合適或者計算的誤差和失誤等有關,可以通過改善上面的因素直到有分布模型符合以上兩點判據。


K-S 檢驗法進行檢驗,且伽瑪分布的統計量K-S 檢驗法Dmax的值最小,其概率密度函數的誤差平方和也是最小的,所以我們確定該銑削電主軸載荷譜的分布模型為伽瑪分布,其形狀參數為4. 7,尺度參數為0. 077。
5 可靠性試驗加載譜的編制
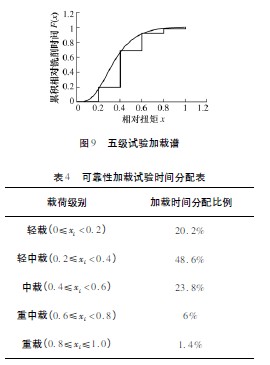
國產170XD30 銑削電主軸載荷譜的分布為伽瑪分布,伽瑪分布函數曲線是一根連續的曲線,不可能完全按照這根曲線來進行電主軸的可靠性試驗加載,通常將其分成幾個載荷級別。對電主軸載荷級別的劃分我們根據相對銑削扭矩的大小,提出了五級試驗加載譜,輕載、輕中載、中載、重中載和重載這5 個級別的概念[1],具體的劃分處理如下: 當0≤xi< 0. 2 時,按輕載歸類; 當0. 2≤xi < 0. 4 時,按輕中載歸類; 當0. 4≤xi < 0. 6 時,按中載歸類; 當0. 6≤xi < 0. 8 時,按重中載歸類; 當0. 8≤xi≤1. 0 時,按重載歸類; 每個載荷級別對應的相對銑削時間將作為可靠性試驗時間分配比例的依據。
五級試驗加載譜如圖9 中的折線所示。表4 是根據五級試驗加載譜具體制定的該電主軸可靠性加載試驗時間分配比例。從表4 可以看出,該電主軸的載荷級別主要是處在輕中載級別,而重載級別時間比例占據較小。
6 結論
1) 采集載荷數據是通過工藝分析計算獲取,這種載荷數據采集的方法克服了現場測試數據的缺陷,使獲得的抽樣樣本足夠大、精確度高,由此建立的載荷譜具有真實性、典型性。
2) 本文中建立的國產170XD30 銑削電主軸的載荷譜是形狀參數為4. 7,尺度參數為0. 077 的伽瑪分布,該載荷譜為電主軸的可靠性實驗首次提供了基礎載荷數據。基于該載荷譜所制定的五級試驗加載譜,可用于該電主軸的可靠性加載實驗。
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com










